25 ++ (a+b+c+d)^3 formula 326704-What is formula of (a+b+c)3

Cubic equations take the form a x 3 b x 2 c x d = 0 {\displaystyle ax^ {3}bx^ {2}cxd=0} However, the only essential requirement is x 3 {\displaystyle x^ {3}} , which means the other elements need not be present to have a cubic equation If your equation does contain a constant (a d {\displaystyle d}좌표평면 에서의 곱셈공식의 의미 m ( a ± b ) = m a ± m b {\displaystyle \,m (a\pm b)=ma\pm mb} ( a b ) ( c d ) = a c a d b c b d {\displaystyle \, (ab) (cd)=acadbcbd} ( a b ) 2 = a 2 2 a b b 2 {\displaystyle \, (ab)^ {2}=a^ {2}2abb^ {2}}Simplify fractions and/or signs x = 4 ± 11 which becomes x = x = Example 2 Find the Solution for 5 x 2 x 32 = 0 , where a = 5, b = and c = 32, using the Quadratic Formula x = − b ± b 2 − 4 a c 2 a x = − ± 2 − 4 ( 5) ( 32) 2 ( 5) x = − ± 400 − 640 10

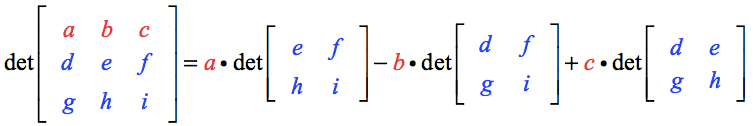
Determinant Of 3x3 Matrix Chilimath

What is formula of (a+b+c)3

What is formula of (a+b+c)3-C Writing the number of each kind of atom as a righthand subscript gives P 4 S 3 as the molecular formula b A Ethyl alcohol contains predominantly carbon and hydrogen, so it is an organic compound B The formula for an organic compound is written with the number of carbon atoms first,Si dice che quattro numeri reali positivi a, b, c, d sono in proporzione fra loro, se il rapporto fra il primo e il secondo è uguale al rapporto tra il terzo e il quarto;

Safe Sums Across Columns In Dataiku Dss Formulas Dataiku Academy 8 0 Documentation

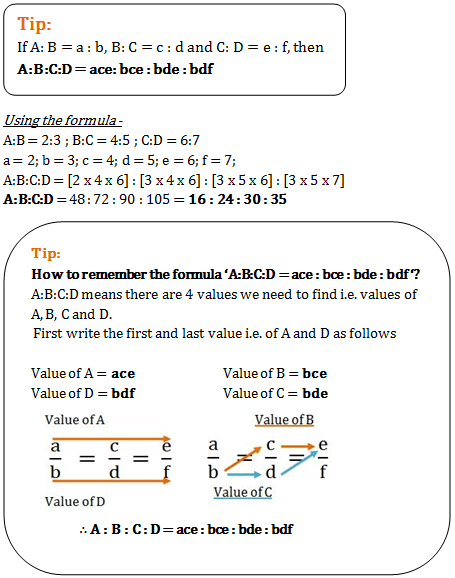
Ex 31 , 7Find the value of a, b, c, and d from the equation 8(a−b&2ac@2a−b&3cd) = 8(−1&5@0&13)Since matrices are equalTheir corresponding elements are equal a − b = −1 2a − b = 0 2a c = 5 3c d = 13Solving these equationsFrom (2) 2a − b = 0 2Binomial Theorem (ab)1 = a b ( a b) 1 = a b (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (ab)3 = a3 3a2b 3ab2 b3 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3 (ab)4 = a4 4a3b 6a2b2 4ab3 b4 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4If A B = 3 4, B C = 5 7 and C D = 8 9 then A D is equal to A10 21 B21 10 C3 7 D7 3 Show Answer 10 21 Hence option A is the right answer

A 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcA b c d e 1 1 0 2 2 0 3 3 4 4 7 5 5 3 6 6 2 7 7 2 8 8The molecular formula for butane is C 4 H 10 The ratio of carbon atoms to hydrogen atoms in butane is 410, which can be reduced to 25 The empirical formula for butane is therefore C 2 H 5 The formula unit is the absolute grouping of atoms or ions represented by the empirical formula of a compound, either ionic or covalent

Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 answer choices a = 4, b = 8, c = 3 a = 4, b =8, c =3 a = 4, b = 8, c = 3 a = 4, b = 8, c = 3 s Question 2A^3 b^3 c^3 = d^3 Reading about Fermat's Last Theorem again, and once again I find myself wondering about positive integer solutions of a 3 b 3 c 3 = d 3Exercise 3 Find a real root of the cubic equation in Exercise 2 (This is for practice purposes only;

Solved 3 Determine Constants A B C D And E That Will Chegg Com

What Is The Most Precise Name For Quadrilateral Abcd With Vertices A 5 7 B 6 3 C 10 2 And Brainly Com

A^2 – b^2 = (a – b)(a b) (ab)^2 = a^2 2ab b^2;A Pythagorean triplet is a set of three natural numbers, a < b < c, for which, a 2 b 2 = c 2 For example, 3 2 4 2 = 9 16 = 25 = 5 2 There exists exactly one Pythagorean triplet for which a b c = 1000 Find the product abc Source http//projecteulernet/indexphp?section=problems&id=9 I tried but didn't know where my code went wrongEx 31 , 7Find the value of a, b, c, and d from the equation 8(a−b&2ac@2a−b&3cd) = 8(−1&5@0&13)Since matrices are equalTheir corresponding elements are equal a − b = −1 2a − b = 0 2a c = 5 3c d = 13Solving these equationsFrom (2) 2a − b = 0 2

Http Jbeach Weebly Com Uploads 8 5 2 1 1 1 M 1 Sequence Wks Pdf

How To Find The Value Of A B C D If A B C D Are The Roots Of Equation X 3x 1 Quora

A^2 b^2 = (a – b)^2 2ab좌표평면 에서의 곱셈공식의 의미 m ( a ± b ) = m a ± m b {\displaystyle \,m (a\pm b)=ma\pm mb} ( a b ) ( c d ) = a c a d b c b d {\displaystyle \, (ab) (cd)=acadbcbd} ( a b ) 2 = a 2 2 a b b 2 {\displaystyle \, (ab)^ {2}=a^ {2}2abb^ {2}}1 Answer Massimiliano · David Y Feb 3, 15 The answer is (a b)3 = a3 3a2b 3ab2 b3 It's easy to prove (a b)3 = = (a b)(a b)(a b) = = (a2 ab ab b2)(a b) = = (a2 2ab b2)(a b) =

Ib Chemistry Assignment 1 Name Write The Formulas Of The

What Is The Expansion Of A B C 3 Quora

La formule du binôme de Newton est une formule mathématique donnée par Isaac Newton pour trouver le développement d'une puissance entière quelconque d'un binôme Elle est aussi appelée formule du binôme ou formule de NewtonIn formula a b = c d oppure a b = c d {\displaystyle ab=cd\quad {\mbox{oppure}}\quad {\frac {a}{b}}={\frac {c}{d}}}Formula Sheet 1 Factoring Formulas For any real numbers a and b, (a b)2 = a2 2ab b2 Square of a Sum (a b)2 = a2 2ab b2 Square of a Di erence a2 b2 = (a b)(a b) Di erence of Squares a3 b3 = (a b)(a2 ab b2) Di erence of Cubes a3 b3 = (a b)(a2 ab b2) Sum of Cubes 2 Exponentiation Rules For any real numbers a and b, and any rational numbers p q and r s,

What Is The Perfect Formula For A B C Cube Quora

What Is The Formula For Math A B C 3 Math Quora

Answer answered On a coordinate plane, 3 triangles are shown Triangle B C D has points (1, 4), (1, 2), (5, 3) Triangle B prime C prime D prime has points (negative 1, 4), (negative 1, 2), (negative 5, 3) Triangle B doubleprime C doubleprime D doubleprime has points (5, negative 1), (5, negative 3), (1, negative 2) Which rule describes theSimplify fractions and/or signs x = 4 ± 11 which becomes x = x = Example 2 Find the Solution for 5 x 2 x 32 = 0 , where a = 5, b = and c = 32, using the Quadratic Formula x = − b ± b 2 − 4 a c 2 a x = − ± 2 − 4 ( 5) ( 32) 2 ( 5) x = − ± 400 − 640 10Ex 31 , 7Find the value of a, b, c, and d from the equation 8(a−b&2ac@2a−b&3cd) = 8(−1&5@0&13)Since matrices are equalTheir corresponding elements are equal a − b = −1 2a − b = 0 2a c = 5 3c d = 13Solving these equationsFrom (2) 2a − b = 0 2

Show That Points A 3 2 B 1 2 And C 9 10 Are Collinear Sarthaks Econnect Largest Online Education Community

If A 3 2 B 1 0 And C 1 12 Are The Vertices Of A Triangle And D Is The Midpoint Of Find The Brainly In

Equation A \( x^2 5x 2 = 0 \), here \( a = 1 \), \( b = 5 \) and \( c = 2 \) Equation B \( 3x^2 x 9 = 0 \), here \( a = 3 \), \( b = 1 \) and \( c = 9 \) Equation C \( x^2 9 = 0 \), here \( a = 1 \), \( b = 0 \) and \( c = 9 \)Equation A \( x^2 5x 2 = 0 \), here \( a = 1 \), \( b = 5 \) and \( c = 2 \) Equation B \( 3x^2 x 9 = 0 \), here \( a = 3 \), \( b = 1 \) and \( c = 9 \) Equation C \( x^2 9 = 0 \), here \( a = 1 \), \( b = 0 \) and \( c = 9 \){a,d,e} {b,d,e} {c,d,e} It has rejected any with a and b, or a and c, or b and c, or even all three a,b and c So {a,d,e) is allowed (only one out of a,b and c is in that) But {b,c,d} is rejected (it has 2 from the list a,b,c)

Solved 1 Consider The Equation A B C D 8 A How Many S Chegg Com

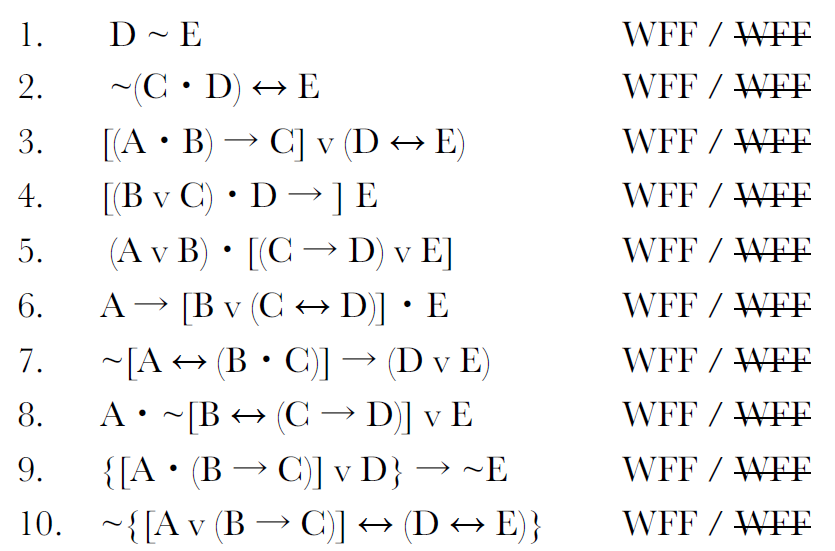
Solved Determine Whether Each Compound Statement Is A Wel Chegg Com

To make the computations a little less messy, the root will turn out to be an integer, so one could use the Rational Zero test instead) Answer Next The Geometry of the Cubic Formula Trigonometry Complex Variables(parfois aussi notés C kФормулы для кубов ( a ± b ) 3 = a 3 ± 3 a 2 b 3 a b 2 ± b 3 {\displaystyle (a\pm b)^ {3}=a^ {3}\pm 3a^ {2}b3ab^ {2}\pm b^ {3}} a 3 ± b 3 = ( a ± b ) ( a 2 ∓ a b b 2 ) {\displaystyle a^ {3}\pm b^ {3}= (a\pm b) (a^ {2}\mp abb^ {2})}

You Are Given The Electronic Configuration Of Five Neutral Atoms

Open Lib Umn Edu App Uploads Sites 2 19 06 Vector Form Of Area Pdf

(a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 (a b – c) 2 = a 2 b 2 c 2 2ab – 2bc – 2ca (a – b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2ca (a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca;In formula a b = c d oppure a b = c d {\displaystyle ab=cd\quad {\mbox{oppure}}\quad {\frac {a}{b}}={\frac {c}{d}}}HO, the empirical formula, tells you the proportion in which each element is present in a given molecule In this case, it tells you that there is an Hydrogen atom for each Oxygen atom The proportion is 11 So, this empirical formula could refer to HO, H2O2, H3O3, and so on OTHER SETS BY THIS CREATOR

Amazon Com Men S Multivitamin Advanced Formula With Zinc A B C D3 E Vitamins Daily Supplement For Heart Health Support Promotes Mental Clarity Focus For Whole Body Health 30

Multinomial Expansion

Answer is very simple Given Expression = sum of the square of all variables 2 a ( Sum of all the terms except the terms a and before a ) 2 b ( Sum of all the terms except b and those before b) 2c ( Sum of all the terms expect c and those before c) 2m (Sum of all the terms expect m and before m )(abc)^3 Formula A Plus B Plus C Whole Square (abc)^3 Proof = a^3 b^3 c^3 6abc 3ab (ab) 3ac (ac) 3bc (bc)Si dice che quattro numeri reali positivi a, b, c, d sono in proporzione fra loro, se il rapporto fra il primo e il secondo è uguale al rapporto tra il terzo e il quarto;

Chapter 22

Academic Oup Com Ptp Article Pdf 13 4 405 13 4 405 Pdf

The cubic then has the form a(xx1)(xx2)(xx3) Multiplying out we obtain ax3a(x1x2x3)x2a(x1x2x1x3x2x3)xa x1x2x3 Thus setting b=0 (depressing the cubic) means x1x2x3=0, and vice versa A cubic (in black) and its depressed counter part (in blue) Note that the roots of the depressed cubic add up to 0Cos (A B) = Cos A Cos B Sin A Sin B Start with cosine of angle A and multiply it with cosine of angle B and in other part i e After ve sign Start with Sine of angle A and multiply with Sine of angle B i 1 st and 2 nd terms are cosine and 3 rd and 4 th terms are sine , and angles start with A then B again A then again BÉnoncé Si x et y sont deux éléments d'un anneau (par exemple deux nombres réels ou complexes, deux polynômes, deux matrices carrées de même taille, etc) qui commutent 2 (c'estàdire tels que xy = yx — par exemple pour des matrices y = la matrice identité) alors, pour tout entier naturel n, () = ∑ = − = ∑ = −,où les nombres =!!

Find The Area Of A Quadrilateral Abcd In Which Ab 3 Cm 4 Cm Cd 4 Cm Da 5 Cm And Ac 5 Cm Cbse Class 9 Maths Learn Cbse Forum

What Is The Expansion Of A B C 3 Quora

A plane in threedimensional space has the equation a x b y c z d = 0, ax by cz d=0, ax bycz d = 0, where at least one of the numbers a, b, a, b, a,b, and c c c must be nonzero A plane in 3D coordinate space is determined by a point and a vector that is perpendicular to the planeBinomial Theorem (ab)1 = a b ( a b) 1 = a b (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (ab)3 = a3 3a2b 3ab2 b3 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3 (ab)4 = a4 4a3b 6a2b2 4ab3 b4 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4

Solution A B C D And E Are Consecutive Points On A Line If Ab 1 3 Cd 1 4 And Cd De 1 2 What Is Ac Be How Would I Set Up This Problem In Order To

A Physical Quantity X Is Given By X b3 C D If The Percentage Errors Of Measurement In A B C And D Are 4 2 3 And 1 Respectively Then Calculate The Er Physics Topperlearning Com Xgiw04pp

3 5 Solution By Determinants The Determinant Of A Matrix The Determinant Of A Matrix A Is Denoted By A Determinants Exist Only For Square Matrices Ppt Download

Top 10 Best Ab Vitamin D3 Supplements Bestgamingpro

Standard Ch 3 A B C D The Student Will Investigate And Understand

Prove That The Points A 2 3 B 2 2 C L 2 And D 3 1 Are The Vertices Of A Square Abc Brainly In

Discount On Organic Chemistry Test Bank 14 By Quickmail710 Issuu

Math 105 Final Exam Give The Formula For The Sum Your Dreams Our Miss

C Ch C Chu Dj Ch Cho 1 A B C 2 C D 3 A

What Is The Number Of Terms In A B C D 3 Quora

Show That The Points A 2 2 B 14 10 C 11 13 And D 1 1 Are The Vertices Of A Rectangle Brainly In

Ex 10 1 9 Without Using Distance Formula Show That Ex 10 1

19 In The Following Table Six Elements A B C D E And F Here Letters

Goldstein Poole Schmidt Chapter 4 Docsity

If A B C D Then Prove That A 2 C A C 2 B 2 D B D 2 A C 3 B D 3 Mathematics Topperlearning Com 9dnawz55

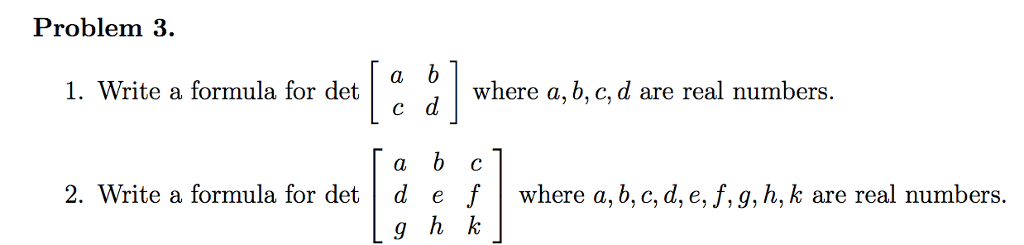
Solved Write A Formula For Det A B C D Where A B C D Chegg Com

Facts And Formulas Quiz Pdf Document

Answered Ax B 3 Suppose F X Cx D A Find Bartleby

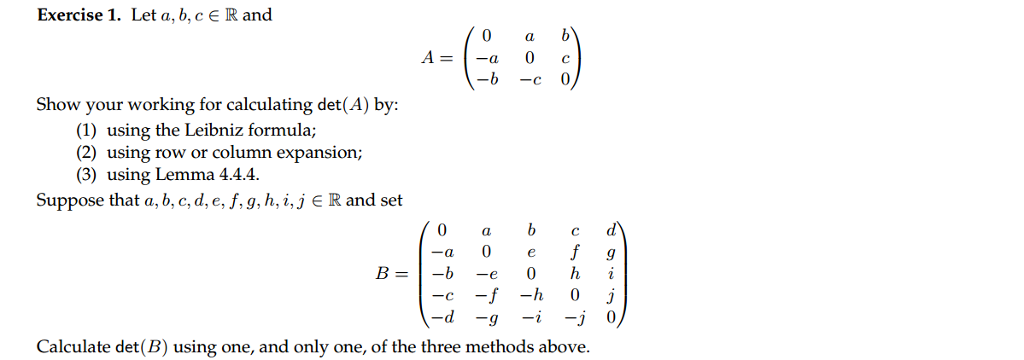
Solved Exercise 1 Let A B Cerand A 0 C Show Your Work Chegg Com

Cbse Class 9 Maths Ncert Solution Heron S Formula Exercise 12 2 Problem 2 Youtube

A Tisket A Tasket An Apollonian Gasket American Scientist

Faculty Math Illinois Edu Hildebr 370 370generalproblemssol Pdf

Solved Hi Help Me With This This Is From Mathematics In Chegg Com

2

Once Daily Multivitamin For Men 50 And Over Supplement For Heart Health Support With Zinc A B C D3 E Vitamins For Memory Brain Health Support Designed

If A B 2 3 B C 5 7 And C D 3 10 Then What Is A D Equal To Quora

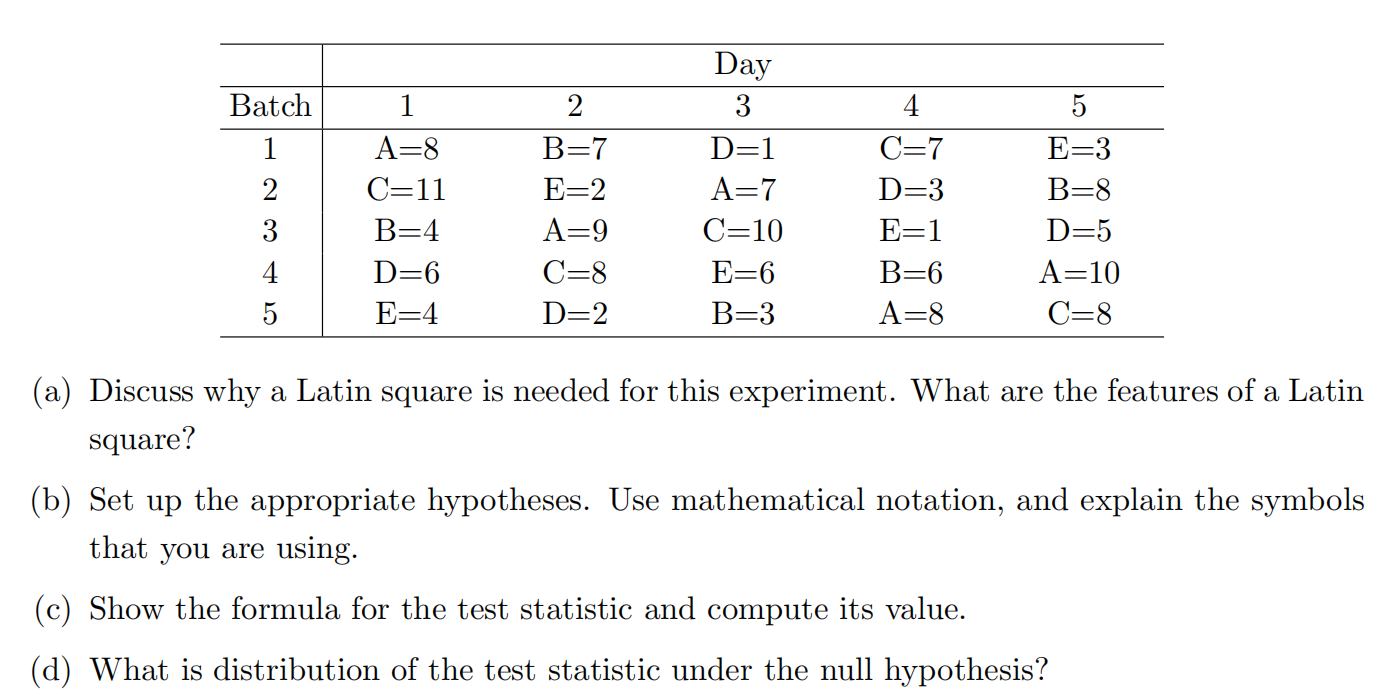
Solved The Effect Of Five Different Ingredients A B C Chegg Com

Click Here Test Bank Doctor

What Is The Expansion Of A B C 3 Quora

Plane And Solid Geometry C A B D C Given A Abc With Sides A And C To Derive A Formula For The Area Of A Abc In Terms Of

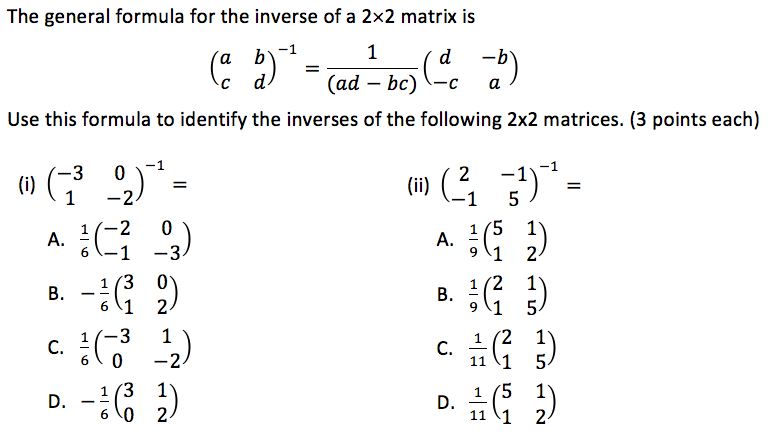
Solved The General Formula For The Inverse Of A 2 Times 2 Chegg Com

If A B C B C D C D A And Abcd Is Not Equal To Zero Then What Is The Value Of A B B C C D D A Mathematics Topperlearning Com 78tjmzhh

Maths Formulas

Http Www Mast Queensu Ca Mikeroth Oldteaching Linalg2 Hmwk Hmwk2 Pdf

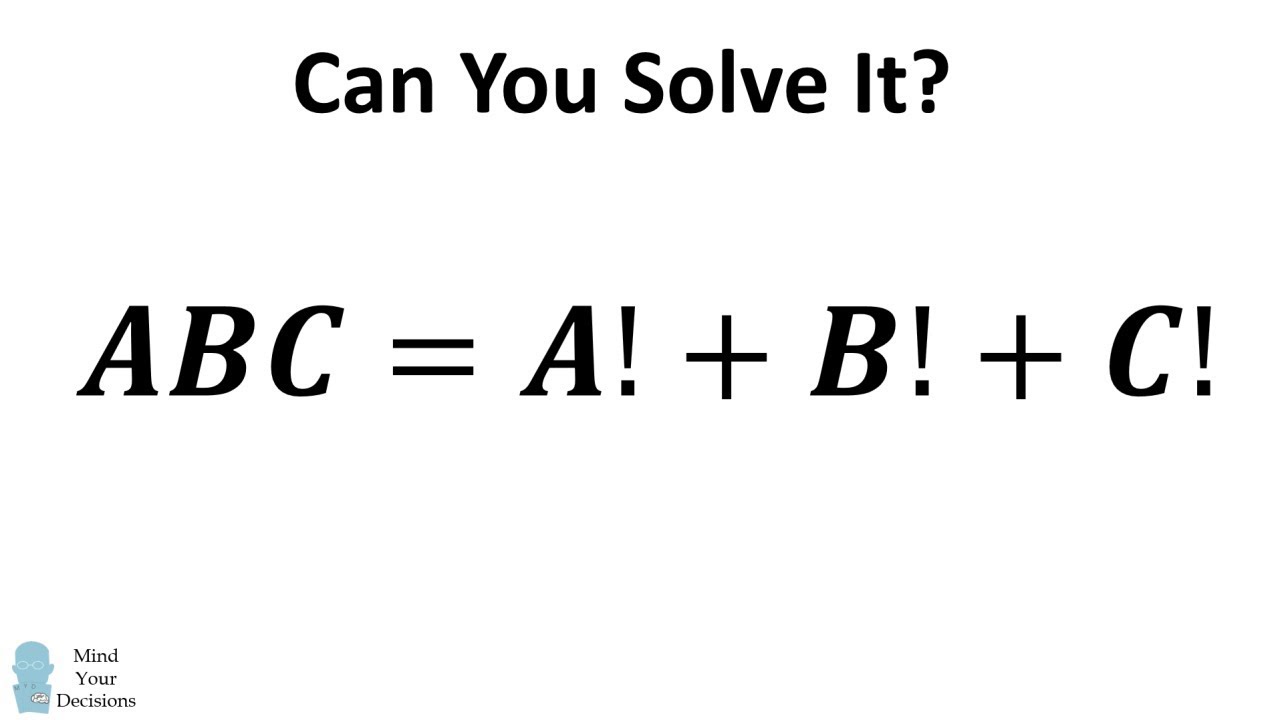
Solve Abc A B C The Factorial Digits Sum Puzzle Mind Your Decisions

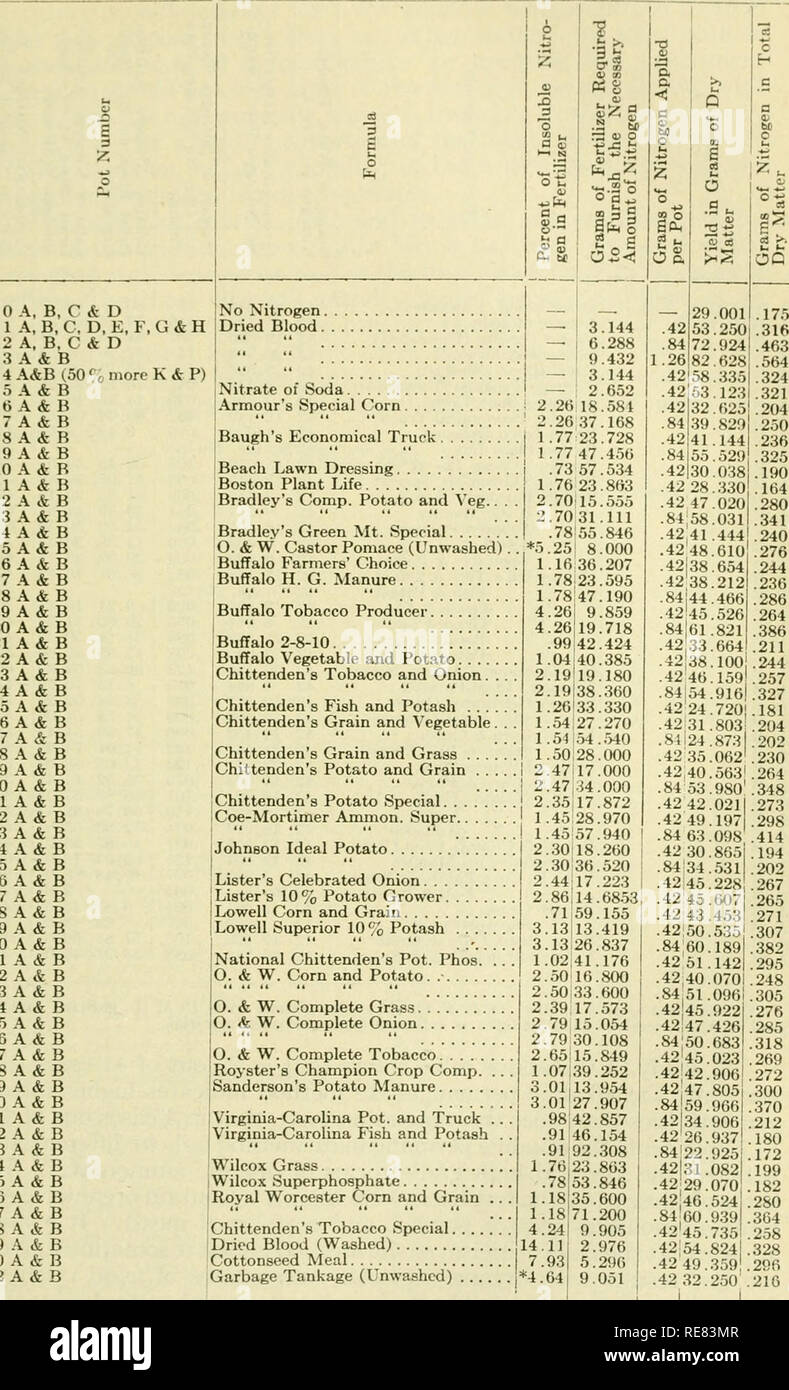
Control Series Bulletin Feeds Fertilizers Table No I 0 A B C Amp D 1 A B C D E F A 2 A B C Amp D 3 A Amp B 4

Name Date Class Review Worksheet

What Is The Expansion Of A B C 3 Quora

Solved Let A B C D Find A 2 Ab Ac Acb Da Let Chegg Com

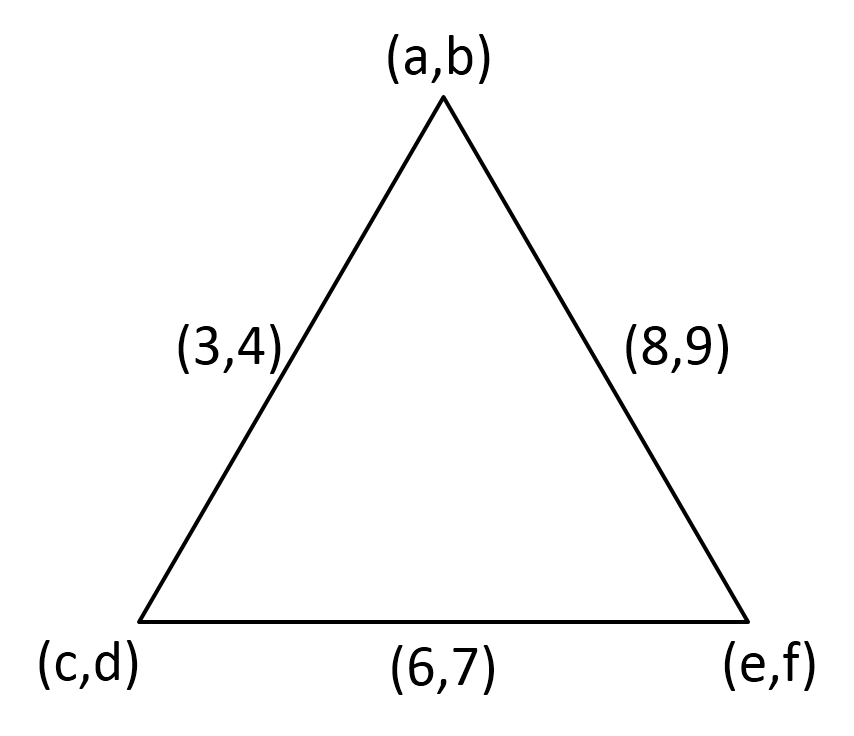
The Midpoints Of The Sides Ca And Ab Of A 8710 Abc Are D 3 4 E 8 9 And F 6 7 Respectively Find The Coordinates Of The Vertices Of The Triangle Mathematics Topperlearning Com Le8c5q

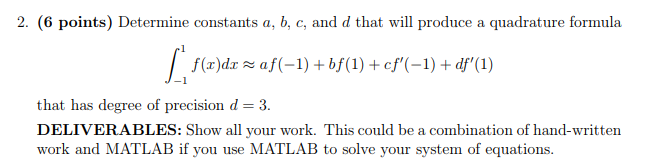
Solved 2 6 Points Determine Constants A B C And D T Chegg Com

Ex 10 1 9 Without Using Distance Formula Show That Ex 10 1

Solved 1 Let A A B C D E B A B C D E F Chegg Com

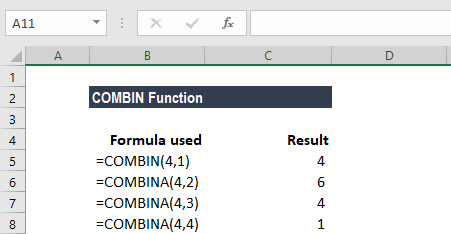
Combin Function Formula Examples How To Use Combin Function

The Electrons In The Atoms Of Four Elements A B C And D Are Distributed

Msbshse Solutions For Ssc Maths Part 2 Chapter 5 Coordinate Geometry

What Is The Expansion Of A B C 3 Quora

What Do M And D Mean In The Formula F A B C D Sigma M 9 10 12 D 3 5 6 7 11 13 14 15 Mathematics Stack Exchange

Quest Set 1

Aptitude Test For Freshers Set 3

7 6 Let X A B C D E F Y 1 2 3 4 Z S Chegg Com

Solved Determine Constants A 6 C And D That Will Produc Chegg Com

Unit 3 Study Guide

Crystallographic Data For The Cd Ii Complex Download Table

Chapter 22 Hw Questions 1 Alkanes Have The General Formula

Solved Problem 1 Let A B C And D Be Invertible Matric Chegg Com

Answered The Formulas Of The Hydroxide Ion The Bartleby

Gcse Changing The Subject Ppt Download

2

How To Auto Sum The Values That Have Been Converted From If Formula Microsoft Community

Chapter 24 Organic Chemistry

Find The Area Of A Quadrilateral Abcd In Which Ab 3 Cm 4 Cm Cd 4 Cm Cbse Class 9 Maths Learn Cbse Forum

Safe Sums Across Columns In Dataiku Dss Formulas Dataiku Academy 8 0 Documentation

What Is The Formula For Math A B C 3 Math Quora

Search Q A 5e3 2bb 5e3 2bc 5e3 Tbm Isch

Find The Volume Of The Tetrahedron Having The Given Vertices 6 6 5 4 6 3 Homeworklib

A B C D E 3

From The Set A B C D E F Find No Of Arrangements For 3 Alphabets With No Data Repeated Brainly In

7 In The Following Table Seven Elements A B C D E F And G Here

Maths Formulas For Cat Euclidean Geometry Euclidean Plane Geometry

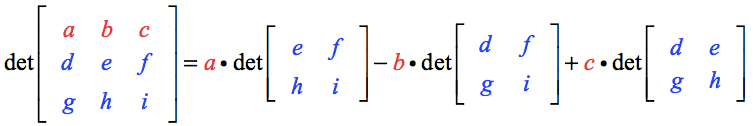
Determinant Of 3x3 Matrix Chilimath

Solved Problem 2 40 Points Let A B C D Er Be Such T Chegg Com

Search Q 3 Example Of Multinomial Tbm Isch

Magic Formula An Overview Sciencedirect Topics

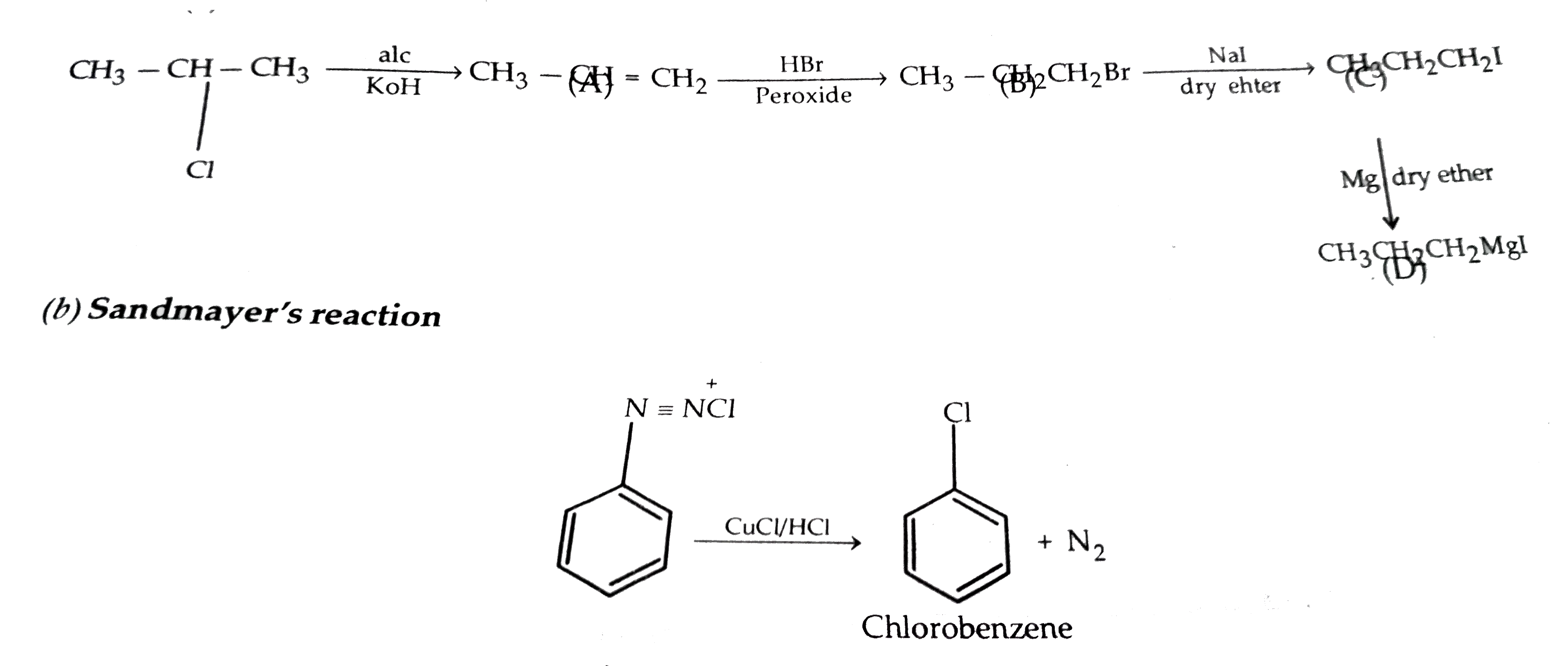
A Write The Structural Formula Of A B C And D In The Following

Multinomial Expansion

A Write The Structural Formula Of A B C And D In The Following

2

Pdf The Koide Lepton Mass Formula And Geometry Of Circles

Ab If The Formula For A Physical Quantity Is X And If The Percentage Error In

What Is The Expansion Of A B C 3 Quora

A B C D 2

Solved Given The Following Boolean Function In Sum Of Pro Chegg Com

Solved If A Is The 2 2 Matrix Given By A A B C D And Chegg Com

Incoming Term: (a+b+c+d)^3 formula, what is a 3 b 3 formula, what is (a+b)^3 formula, what is formula of (a+b+c)3, how many types of a b c d, d=abc what is the formula for c,